Ядерное множество.

Определение

    A. Набор n ядер (структур D.p/n)  Dpn, упорядоченных по натуральному числу n, называется  ядерным множеством.

     B. Набор n изолированных и упорядоченных по натуральному числу n ядер (структур)  Dpn , каждое из которых представлено одинаковыми взаимодействующими единичными элементами n,  дефектами  D и формой p называется  ядерным ножеством.         

    http://www.appp.org.ua                       Буртыка М.В.                                         

   Простейшее модельное представление включает ряд структур показанных на рис.1.

   Здесь: D – целое число, определяющее количество дефектов ( ЕД - единичных дефектов или d , рис.2) конкретного ядра; n – число составляющих ядро частей (ЕЭ - единичных элементов или N, рис.3); p – число частей ЕЭ, образующих форму ядра. Ядро состоит из дефектов и единичных элементов ЕЭ. Структурную формулу ядра Dpn  можно записывать в более удобном виде D.p/n. Так на рис.1 представлен ряд ядер: 133, 244, 3.5/5, 4.6/6, 6.6/7.

  Запись  множества структур в виде таблицы 1 позволяет системати­зировать многие  внешние и внутренние свойства последних.  

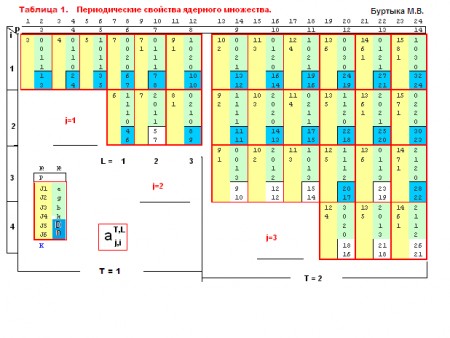
На   Натуральные числа D, p, n подчиняются  периодическим зависимостям типа:

ти

p(T,L,j,I)= 3j + (L-1),

n(T,L,j,I) =3j(j-1)/2 + 2(j-i) – (T-2) + {(2T-1) + [j – (2T-1)](L-2)}(L-1),

2.       Упорядоченное по таблице множество,  наделяет единичные элементы ядер набором конкретных физических свойств: A, B, C, E таких, что межэлементные взаимодействия в каждом из ядер полностью описываются девятью квантами взаимодействия: A^A, A^B, A^C, B^B, B^C, B^E, C^C, C^E, E^E. Эти величины образуют треугольную 4х4 матрицу

        A=a(r,s), которая является константой таблицы.

3.       Ядро характеризуется 15 величинами, и только 4-е  из них:e, g, b, k являются независимыми и определяют структурную симметрию. Через выделенные коэффициенты симметрии выражаются все остальные свойства ядра: структурные -

               n=(e+g+k+2b–1)(g+k+b–1)+b(e+g+b)–k(k–1)/2            

      и

       p= 2(e+2g)+3(2b+k–2)

 и др.; математические – координатная система ядра, координаты ЕЭ  xn(e, g, b, k)   и   др. в ядерном базисе; физические – свойства ЕЭ, число квантов взаимодействия в конкретном ядре     n AA, n AB, .... Последние образуют 4х4 симметрическую треугольную  матрицу  N= n(r,s),  которая  является  константой конкретного ядра.

.           След от произведения  матричных констант таблицы и ядра определяет  энергию элемента ядерного множества:

 Здесь d - энергетическая константа таблицы и все кванты взаимодействия пропорциональны её значению.

6.        Ядро является динамичным объектом с большим числом статических и возбужденных состояний. Переход из одного статического состояния в другое происходит через возбужденное состояние. Для конкретного ядра с заданным  n, статические состояния отличаются величинами p и D, коэффициентами симметрии и набором квантов взаимодействия. Энергетический спектр модели является дискретным и обусловлен  изменением числа D при переходах между состояниями.  Наличие противоположных состояний ядра (статических и возбужденных) способствует их распаду и объединению.

7.        Возбужденные состояния структур подчиняются тем же табличным закономерностям и характеризуются числами заполнения a - слоев (орбит):  1 n 6 и m a: 

nЕЭ = (3+ n -2) –m + 1 + n,5  ,  =1,2,3.., n=0,1,2,,,5, m=1,2,3...

Формулы заполнения слоев ЕЭ:

J1m,n=n+0,n,

J+1m,n=n+6+=1(1+, + m,),           = + n,5 -  n,0,  =1,2,..-1.

Аналогичным поведением характеризуются и последующие возбуждения. Максимальное число возбуждений  каждой структуры определяется разностью n - p.